The Collatz Problem
While not technically an automata, I have often marveled at the Collatz Problem. You can learn more information about it here at the AT&T Integer Sequences On-Line Database.
The Problem
The problem works in a recursive manner:
- Given a positive integer.
- If the integer is even, divide it by two.
- If the integer is odd, multiply it by 3 and add 1.
- Go back to step 1.
So consider the sequence when starting at 1: 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, …
Now consider the sequence when starting at 10: 10, 5, 16, 8, 4, 2, 1, …
So given a positive integer, it would appear the steps above would eventually fall into an infinitely repeating pattern upon reaching 1. Whether this is truly the case remains an open problem.
The Interest
Another open problem is predicting the number of iterations required to reach 1. This is something that piques my curiosity. Consider more sequences and the following table:
1
2, 1
3, 10, 5, 16, 8, 4, 2, 1
4, 2, 1
5, 16, 8, 4, 2, 1
6, 3, 10, 5, 16, 8, 4, 2, 1
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
| Number | Count |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 7 |
| 4 | 2 |
| 5 | 5 |
| 6 | 8 |
| 7 | 16 |
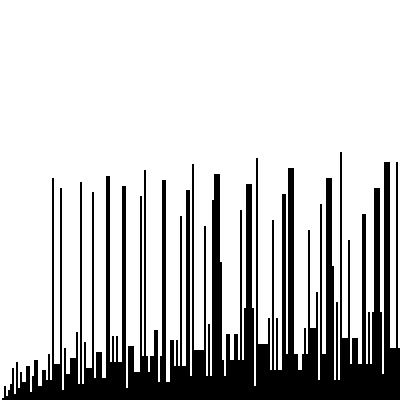
Wondering what the graph would look like, I used my drawing utility for automata to create the following:
The horizontal axis corresponds to sequential integers starting at 1 and the vertical axis corresponds to the count of iterations required before reaching 1 (as in the table above). As you can see, the graph appears chaotic.
The Code
// Author: Grant Jenks // File: Collatz.cs // Build: csc.exe /R:Automata.Draw.dll Collatz.cs // Run: Collatz.exe // View: Collatz.jpg // Copyright 2009 using System.Drawing; namespace Automata { class Collatz { public static void Main ( string[] args ) { // Note that we might index outside of the "values" array if // the iteration count happens to be greater than "size". // There is nothing which requires the graph to be square // or otherwise. In fact, if "size" is set to 100, overflow // will occur. It just so happens that no integer between // 1 and 200 will require more than 200 iterations to reach // 1 when applying the Collatz algorithm to it. const int size = 200; int[,] values = new int[size, size]; // Fill the zeroth row with a count of iterations required // to reach 1 according to the Collatz Problem. The integer // sequence is described in detailed here: // http://www.research.att.com/~njas/sequences/A006577 for (int i = 0; i < size; i++) { int count = 0; int current = i+1; while (current != 1) { if (current % 2 == 0) { current /= 2; } else { current = current * 3 + 1; } count++; } values[0, i] = count; } // Now make the values array into a kind of bar graph by // filling each column with 1's equal to the count in the // zeroth row. for (int i = 0; i < size; i++) { int count = values[0, i]; for (int j = 0; j < count; j++) { values[j, i] = 1; } } // This simple viewer draws White for each 0 and Black for // each non-zero value. Automata.Draw.Viewer viewer = (i => i == 0 ? Color.White : Color.Black); Automata.Draw.Write("Collatz.jpg", size, 2, values, viewer); } } }