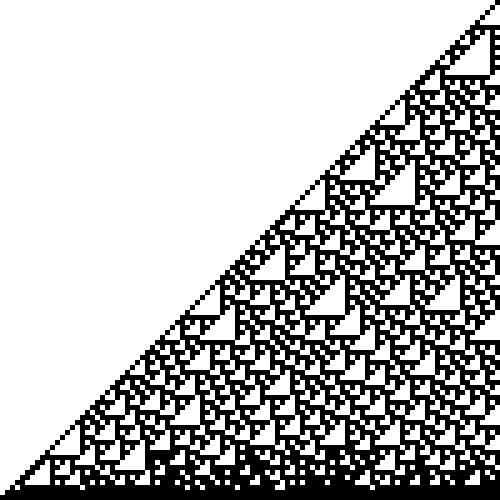
Absolute Differences Between Consecutive Prime Numbers
Background
Consider the following sequence:
2, 4, 6, 8, …
Can you spot the pattern? How about this one:
4, 9, 16, 25, …
Or this one:
4, 27, 256, 3125, …
Now imagine you took the difference between consecutive values. In the first case, it get's boring quickly:
| 0 | 0 | ||
| 2 | 2 | 2 | |
| 2 | 4 | 6 | 8 |
In the second case, it's a little more interesting:
| 0 | |||
| 2 | 2 | ||
| 5 | 7 | 9 | |
| 4 | 9 | 16 | 25 |
And in the third case, it's much more interesting:
| 2434 | |||
| 206 | 2640 | ||
| 23 | 229 | 2869 | |
| 4 | 27 | 256 | 3125 |
What we're doing here by taking the difference is actually taking the derivative. So in the first case, where numbers rise linearly, the derivative is a constant and its derivative is zero. In ths second case, where numbers rise by the square, the first derivative shows a similar linear pattern to the first case. The last case is exponential and its analysis is beyond the scope of this page.
Now consider the sequence of primes: 2, 3, 5, 7, … Do they grow linearly? quadratically? exponentially? While it can be proved that the primes are bounded by logarithmic functions, it is impossible to formulate an equation for the n'th prime. What would it look like if we took the derivatives as we did before:
| 1 | 2 | 0 | 0 | 0 | 0 | |||
| 1 | 0 | 2 | 2 | 2 | 2 | 2 | ||
| 1 | 2 | 2 | 4 | 2 | 4 | 2 | 4 | |
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
That doesn't make much sense at all. (There are no negative numbers because the absolute difference is taken between consecutive cells.) Now imagine non-zero squares were colored black and the rest white. What would it look like? Would a pattern emerge? The below images show the answer to just such questions.
Absolute Differences Between the First 100 Consecutive Prime Numbers
Absolute Differences Between the First 500 Consecutive Prime Numbers
The Code
// Author: Grant Jenks // File: PrimeDiffAbs.cs // Build: csc.exe /R:Automata.Draw.dll PrimeDiffAbs.cs // Run: PrimeDiffAbs.exe // View: PrimeDiffAbs.jpg // Copyright 2009 using System; using System.Drawing; namespace Automata { class PrimeDiffAbs { public static void Main(string[] args) { // Size represents the number of primes we will initially generate // and use to seed the initial row of the values grid. const int size = 100; int[,] values = new int[size, size]; // This algorithm fills in the first row of the values grid with 'size' // prime numbers. In this case, it's 100 prime numbers: 2, 3, 5, 7, ... values[0,0] = 2; for (int i = 1; i < size; i++) { // Get the previous prime number and iterate forward (by adding one) // until the next prime number is found. int next = values[0,i-1]; bool prime = false; while (!prime) { next++; // Determine whether this number is prime. Because multiplication // is commutative, we need only check up to the square root of the // number. prime = true; for (int j = 2; j <= Math.Sqrt(next); j++) { // If a divisor is found then break so that we can iterate // forward to the next number. if (next % j == 0) { prime = false; break; } } } values[0,i] = next; } // Now fill in the rest of the grid as the absolute differece of the // values above and to the right of this value. For instance, if the // cells were initially seeded like this: // 2 3 5 7 // 0 0 0 0 // 0 0 0 0 // 0 0 0 0 // then this algorithm would fill in the rest as such: // 2 3 5 7 // 0 1 2 2 // 0 0 1 0 // 0 0 0 1 for (int i = 1; i < size; i++) { for (int j = i; j < size; j++) { values[i,j] = Math.Abs(values[i-1,j] - values[i-1,j-1]); } } // This viewer maps any zero value to white and non-zero value to black. Automata.Draw.Viewer viewer = (i => (i == 0) ? Color.White : Color.Black); Automata.Draw.Write("PrimeDiffAbs.jpg", size, 5, values, viewer); } } }