Grammar Inductor

I've made some progress on this. It's kind of cool. I have three tools now:

• Tokenizer
• Sequitur
• Visualizer

Tokenizer uses JTB to translate a minijava program into its tokens. Sequitur looks for patterns and generates a compression grammar for the input stream. Visualizer rewrites the compression grammar for dot.

On my laptop, I can make nifty pictures running the command:

type test\Factorial.java | java -jar jars\Tokenizer.jar | java -jar jars\Sequitur.jar | Visualizer\Visualizer.exe | dot -Tjpg > test\Factorial.java.jpg

Onfortunately, “dot” requires too much memory for some of the tests. I'm still playing with it though.

The Visualizer.exe is written in F#. I'm planning to write other F# programs to do the grammar analysis.

If you are brave, you can see a sample image here.

I wanted to provide an English example so that more people might understand what I'm trying to do. It helps me too!

So imagine you start with a set of English sentences and you're trying to learn the English grammar. You've never been told the English grammar but you know the sentences and have some cool tools.

Here's our English sentences:

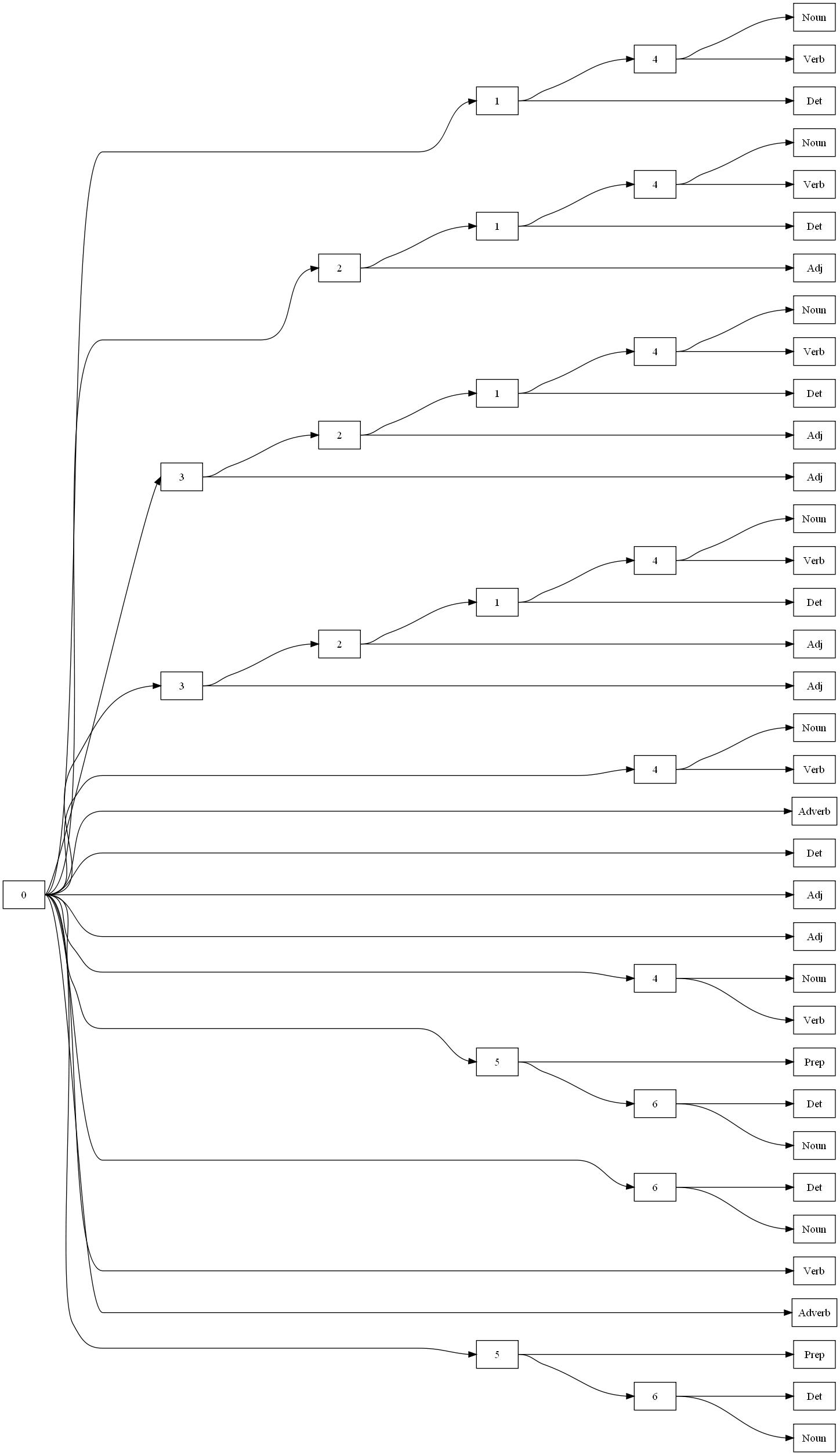
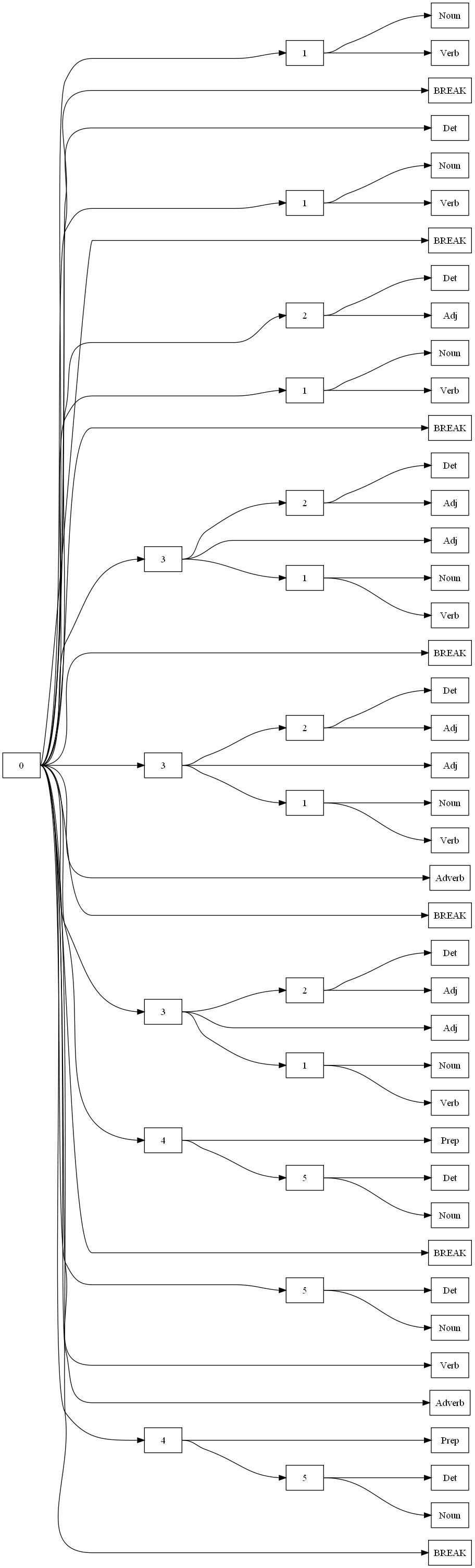
1. Balloons bounce.
2. The balloon bounced.
3. The big balloon bounced.
4. The big red balloon bounced.
5. The big red balloon bounced quickly.
6. The big red balloon bounced in the driveway.
7. The balloon bounced quickly in the driveway.

The “Tokenizer” tool that I created above works to translate the sentences into their parts of speech:

1. Noun Verb
2. Det Noun Verb
3. Det Adj Noun Verb
4. Det Adj Adj Noun Verb
5. Det Adj Adj Noun Verb Adverb
6. Det Adj Adj Noun Verb Prep Det Noun
7. Det Noun Verb Adverb Prep Det Noun

(Note that this is the English equivalent of what it's doing. The real “Tokenizer” is a lexer for the minijava language.)

Now, I create a pre-processing file that I can give to “Sequitur”, and then “Visualizer”, and then “Dot” and out pops this picture:

This one is actually better:

Is structural programming all inclusive? Think of the power of recursion. Hierarchy has to be included.

• sequence
• conditional
• recursion

Algorithm Idea:

1. “Compression and Explanation using Hierarchical Grammars” to induce grammar. Build JavaCC file from this.
2. Process JavaCC file
3. Use SynDiff? to find differences between JavaCC files
4. Use SynDiff? results to “SynMerge” JavaCC files
5. repeat

Methods of combination:

• linear - combine each new sentence example with existing best grammar
• exponential - combine new sentences in pairs and then combine those results in pair until best grammar is reached

Algorithm Idea:

1. tokenize java program1
2. feed tokened program1 to compression grammar program
3. tokenize java program2
4. feed tokened program2 to compression grammar program
5. run syndiff on tokened program1 and tokened program2
6. merge grammars according to results of syndiff
7. repeat how?

Tools Available:

• tokenizer for minijava program
• grammar builder for minijava tokens

Idea:

• use a “genetic algorithm” to blend the grammars

Merging grammars:

1. find all rules with same name and production terminals
   • keep these
2. find all rules with same production terminals
   • rename all these rules appropriately
3. find all rules with same eventual production terminals
   • start as small as possible
   • these are a candidate for combination in the grammar via “|”

Theory rules:

lower case letters denote Terminals
upper case letters denote either a Terminal or NonTerminal

Rule 1)
if
R_0 -> A_0, A_1, ... A_N
R_1 -> B_0, B_1, ... B_M
and
{A_x, ... A_y} => c_0, c_1, ... c_n
{B_v, ... B_w} => c_0, c_1, ... c_n
then
R_0 -> A_0, A_1, ... A_x-1 (A_x, ... A_y | B_v, ... B_w) A_y+1 ... A_N
R_1 -> B_0, B_1, ... B_v-1 (A_x, ... A_y | B_v, ... B_w) B_w+1 ... B_M

Rule 2)
if
R_0 -> A_0, ... A_N
R_1 -> B_0, ... B_M
and
{A_0, ... A_N} => c_0, c_1, ... c_n
{B_0, ... B_M} => c_0, c_1, ... c_n
then
R_2 -> R_0 | R_1

Rule 3)
if
R_0 -> A_0, ... A_N | B_0, ... B_M
and
A_x = B_v, A_x+1 = B_v+1, ... A_y = B_w
then
R_0 -> 	(A_0, ... A_x-1 | B_0, ... B_v-1)
	A_x, ... A_y
	(A_y+1, ... A_N | B_w+1, ... B_M)

How do you meaningfully “diff” two grammars? What does it even mean to do so?

If order into sequitur matters, then does it always build the most compact hierarchical grammar?

Example: 2 3 / 1 2 3 / 1 2 3

Grammar: There will be a NT for “2 3” but none for “1 2” unless ”/ 1 2” is added → what happens then?

This would be super cool: Use a genetic algorithm to pick and choose parts of grammars in order to find the best. So like, “breed” grammars together and keep the ones that are best and continue the process.